Homotopy
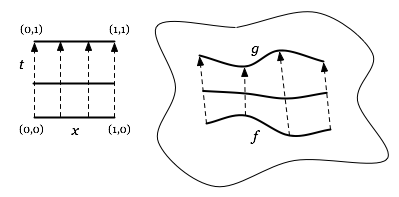
Consider two paths in the same topological space, X. Let's say one is the image of the map f from the interval [0, 1] and the other is the image of the map g from the interval [0, 1].
If it's possible to continuously deform f to g the two are said to be homotopic.
If x is the parameter for a path and t is the parameter for the deformation then we can think of the deformation as a continuous map F : [0, 1] x [0, 1] -> X where
- F(x, 0) = f(x)
- F(x, 1) = g(x)
and F(x, t) for some t, 0 < t < 1 is a path somewhere along in the deformation from f to g.
F is referred to as a homotopy from f to g.
Homotopies, as we shall soon see, will turn out to be a key to the topological difference between a sphere and a torus and will form the basis for our description of the Poincaré Conjecture itself.
UPDATE: next post
Comments (0)
Add a Comment
Last Modified: June 3, 2005
Author: jtauber