Path Homotopy
Previously we defined the notion of homotopy.
Two functions that are continuous deformations of one another are homotopic even if the two functions aren't paths.
But if the two functions are paths, then we can further define a stricter notion called path homotopy.
Two paths are path homotopic iff they are homotopic and they have the same start point and end point throughout the deformation.
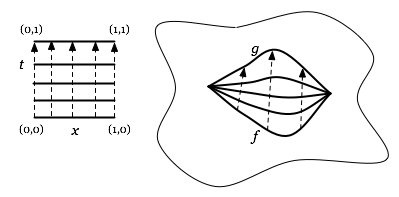
In other words, if our paths are functions f and g from the interval [0, 1] to a topological space X, then path homotopy means not only the existence of a continuous map F : [0, 1] x [0, 1] -> X where
- F(x, 0) = f(x)
- F(x, 1) = g(x)
but also that:
- F(0, t) = f(0) = g(0)
- F(1, t) = f(1) = g(1)
for all t in [0, 1].
UPDATE: next post
Comments (0)
Created: July 1, 2005
Last Modified: July 1, 2005
Author: James Tauber
Last Modified: July 1, 2005
Author: James Tauber