Homotopy Classes and Simple Connectedness

A month ago, we saw that path homotopy provides a way of distinguishing certain topological spaces. We're now in a position to make that a little more precise.

Until now we've not required that our paths end at the same point they start but it's useful at this point to restrict ourselves to such closed paths.

Path homotopy is an equivalence relation which means that we can partition all the closed paths starting and ending at a particular point in a manifold into equivalence classes. Such equivalence classes are called the homotopy classes for that point.

Let's consider again the two manifolds we looked at before that differ only in that the one on the right has a hole in it.

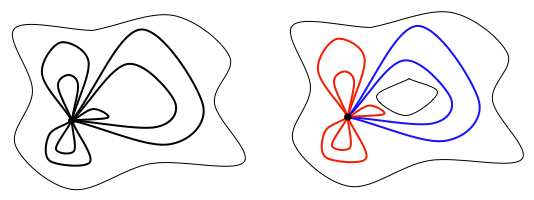
If we pick a point in each manifold, and consider the homotopy classes, we notice something very important. The point in the the manifold on the left has a single homotopy class. All the closed paths shown in black are homotopic. In contrast, the point in the manifold on the right has two homotopy classes. The closed paths in red are homotopic to one another and the closed paths in blue are homotopic to one another but the red paths are not homotopic to the blue paths.

If a topological space is connected and has a single homotopy class for each point, it is said to be simply connected. The manifold on the left is simply connected. The manifold on the right is not.

Another way of thinking about it is that any closed path in a simply connected manifold can be continuously shrunk down to a single point. The paths in red can be continuously shrunk down to a point. The paths in blue cannot. They get "stuck" around the hole.

Simple connectedness is a topological property that distinguishes spaces that may otherwise be topologically equivalent.

We are now ready to state Poincaré's famous conjecture.

UPDATE: next post