Poincare Project: Paths

It's been a while. Back to some topology—we're almost ready to state Poincaré's Conjecture.

Consider drawing a curve on the surface of a object. If we view the surface as a topological space then the curve can be thought of as a set of points in the space with the following property: there exists a continuous function from a closed interval on the reals to that set.

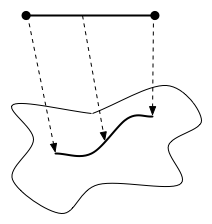
This is the notion of a path. Some topologists will refer to the function as the path while others will refer to the image (i.e. the set of points in the space) as the path. Often it doesn't matter which is meant, e.g. in the sentence "there exists a path between any two points".

Note that there are an infinite number of continuous functions that result in the same image and vary only in the choice of parameterization.

UPDATE: next post