Homotopy as a Way of Distinguishing Topological Spaces

Path homotopy can be used to distinguish topological spaces that otherwise share the same topological properties.

For example, consider two topological spaces the locally resemble R^2 but globally look like the following:

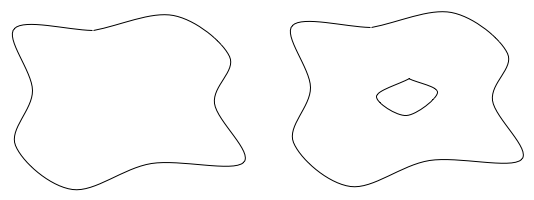
In other words, both are compact manifolds and the one on the right differs from the one on the left in that it has a "hole" in the middle.

Are the two homeomorphic? Our intuition tells us not because of the hole in the one on the right. But if they are not homeomorphic, there must be a topological property that one has that the other does not.

We'll get to what that property is formally later, but for now, I want to show informally that homotopy is the key.

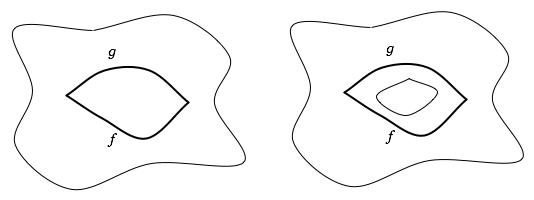
Look at the two paths, f and g on each of the topological spaces. In the space on the left, they are path homotopic whereas on the right, they are not. In other words, the existence of the hole means that not all paths with the same start and end are path homotopic to one another.

There's no way you can continously transform f to g when there is a hole between them.

We'll explore this idea a little more formally over the next couple of weeks and then we'll finally be able to state the Poincaré Conjecture.

UPDATE (2005-07-10): I just changed "homotopic" to "path homotopic" twice in the third last paragraph. It's important that we're talking about path homotopy not just homotopy here as we require the start and end of the path to remain fixed during the transformation from f to g.

UPDATE: next post