Arrow-type Vectors

Part of the Poincaré Project.

When we started to talk about metrics in two or more dimensions I said that "travel in a particular direction at a particular rate" is a kind of vector. This kind of vector can be visualized as an arrow and, with vector addition defined in terms of placing the tail of one arrow at the head of the other, we find that these arrow-type vectors form a linear space.

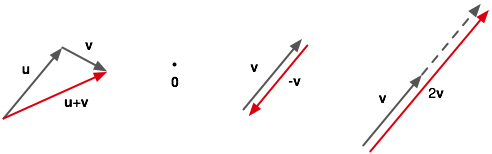
The first diagram shows the way addition is defined. The additive identity (the zero-vector) can then just be thought of as the point in the second diagram. The third diagram shows how inverse of an arrow-type vector falls naturally out of the definition of addition. And finally, the fourth diagram shows scaling. From the axioms we defined for linear spaces we know that v + v = 2v for all linear spaces because v = 1v so v + v = 1v + 1v = (1+1)v = 2v.

Visualizing vectors as arrows is common in introductory approaches to vectors in both mathematics and physics. Displacement, velocity, acceleration, force, etc are often described in these terms. However, there are other physical quantities that, while able to be modeled as objects in linear spaces, are best visualized as something other than arrows. In the next Poincaré Project post, I'll introduce this new type of object that I'll initially call a stack-type vector.

UPDATE: next post