Stack-Type Vectors, Part I
Part of the Poincaré Project...
So I've promised a couple of times to introduce stack-type vectors. This is a type of geometric vector that works a little differently than arrow-type vectors. They still meet the requirements of a linear space but their behaviour on a manifold, in particular with regard to a coordinate system on that manifold is a bit different. We'll get into that difference in subsequent posts (as well as talk about where these stack-type vectors show up in physics).
Here is what a stack-type vector might look like in three-dimensions:

Hopefully you can see why I call these stack-type vectors. From now on, though, we'll mostly draw two-dimensional stack-type vectors, but you should still get the same idea.
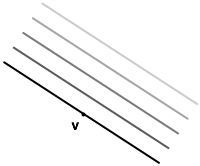
Note that the number of lines drawn and how long they are are not important (any more than the thickness of the line and shape of the arrow are important in an arrow-type vector). Instead it's the direction the lines are stacked in and how tightly they are packed that characterizes the stack-type vector.
But for a set of these to form a linear space, we need to say how to add them and how to scale them.
Here's how this vector scales (by 2x and by -1x):

Notice that scaling by 2x means the lines are packed twice as closely.
In part II, I'll show how addition of these vectors is defined.
The original post was in the category: poincare_project but I'm still in the process of migrating categories over.