Stack-Type Vectors, Part II
Previously, we introduced the stack-type vector and showed the identity vector, how inverses are formed and how these stacks are scaled. We haven't yet show how they are added.
Consider the two stack-type vectors marked (a) and (b) in the diagram below:
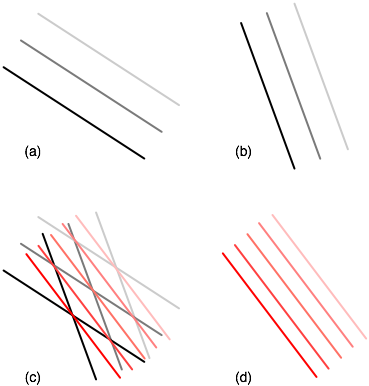
The geometric way stacks are added is to place them on top of each other and draw lines through each point of intersection, as we have done at (c). The resulting lines, show by themselves in (d) are the resultant addition. (Remember the number of lines drawn doesn't matter, it's how dense they are that determines the "magnitude" of the vector)
With a bit of experimentation, you can see that this definition of addition (in the limit as the lines become closer and closer to parallel) fulfills the requirement that v + v = 2v. In fact, you can establish that all the axioms for linear spaces hold true.
So we have so far seen three different types of linear spaces: one type made up of tuples of numbers, one type made up of arrow-type vectors and one type made up of stack-type vectors. The latter two have the special characteristic that they are geometric: they have some meaning in the context of a manifold.
Because physics models phenomena in the physical world (which can be viewed as a manifold) the vectors used in physics are of this geometric type. Displacement, velocity and acceleration are examples of measurements that can be models as arrow-type vectors. But what about stack-type vectors? We'll get to their use in physics in the next Poincaré Project entry.
The original post was in the category: poincare_project but I'm still in the process of migrating categories over.